3.1 LÍMITE DE UNA SUCESIÓN
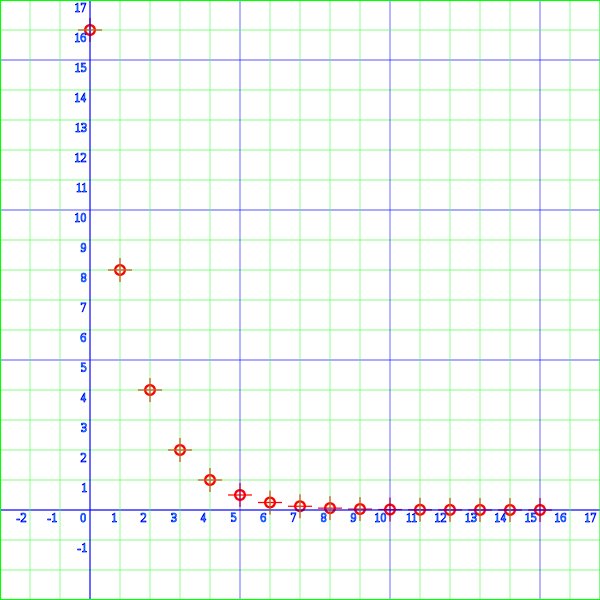
El límite de una sucesión es uno de los conceptos más antiguos del análisis matemático. El mismo da una definición rigurosa a la idea de una sucesión que se va aproximando hacia un punto llamado límite. Si una sucesión tiene límite, se dice que es una sucesión convergente, y que la sucesión converge o tiende al límite. En caso contrario, la sucesión es divergente.
La definición significa que eventualmente todos los elementos de la sucesión se aproximan tanto como queramos al valor límite. La condición que impone que los elementos se encuentren arbitrariamente cercanos a los elementos subsiguientes no implica, en general, que la sucesión tenga un límite.
Véase más en:
3.2 LÍMITE DE UNA FUNCIÓN DE VARIABLE REAL
Se llama función real de variable real a toda aplicación f de un subconjunto no vacío S de R en R.
Una función real está definida, en general, por una ley o criterio que se puede expresar por una fórmula matemática. La variable "x" recibe el nombre de variable independiente y la "y" o f(x) variable dependiente o imagen.
Considérese la función definida por: y= f(x) = 2x²-x-1/x-1 ; x 1 el único punto en el cual f(x) no está definida es en x = 1, pero, en puntos tan cercanos a 1 como se quiera, la función se encuentra definida. Esta situación da lugar a la siguiente pregunta: ¿Se aproxima f(x) a algún valor específico, cuando x se aproxima a 1?
Cuando x se aproxima a 1 por la izquierda (valores menores que 1) y por la derecha de 1 (valores mayores que 1).
a medida que los valores de x, se “acercan” a 1, sin tomar el valor de 1, los valores de f(x) se “acercan” a 3. Dándole a la palabra límite un significado intuitivo, se dice que:
El “límite” de la función f(x) es 3 cuando x tiende a 1. La afirmación anterior frecuentemente se expresa simbólicamente por cualquiera de las formas:
F (x) =3 cuando x–>1 (se lee: f(x) tiende a 3 cuando x tiende a 1).
O también, Lim f (x)=3 ; x–>1 (se lee: límite cuando x tiende a 1 de f(x) es 3). De una manera más general, pero conservando el significado intuitivo de la palabra “límite”, se dice que:
Lim f(x) = L; x–>a, si se puede hacer que f(x) este tan “cerca” de L como se quiera, haciendo que x este suficientemente “cerca” de a, pero siendo distinta de a.
Límite.
Es cuando “X” se aproxima mucho a un valor sin ser el propio valor.
Ejemplos:
- lim x+3/x-4 = lim (1)+3/(1)-4 = 4/-3 = – 4/3
x —- 1
- lim x+3/ x-2 = lim (2)+3/(2)-2 = 5/0 = infinito
x—-2
- lim cos x= cos (0) = 1
x—–0
Ver más en:
3.3 CÁLCULO DE LÍMITES
Si f(x) es una función usual (polinómicas, racionales, radicales, exponenciales, logarítmicas, etc.) y está definida en el punto a, entonces se suele cumplir que:
Es decir: para calcular el límite se sustituye en la función el valor al que tienden las x.
No podemos calcular 
porque el dominio de definición está en el intervalo [0, ∞), por tanto no puede tomar valores que se acerquen a −2.
porque el dominio de definición está en el intervalo [0, ∞), por tanto no puede tomar valores que se acerquen a −2.
Sin embargo sí podemos calcular 
, porque aunque 3 no pertenezca al dominio, D= 
− {2, 3}, sí podemos tomar valores del dominio tan próximos a 3 como queramos.
, porque aunque 3 no pertenezca al dominio, D= − {2, 3}, sí podemos tomar valores del dominio tan próximos a 3 como queramos.
Más en:
3.4 PROPIEDADES DE LOS LÍMITES
Límite de una constante
Límite de una suma
Límite de un producto
Límite de un cociente
Límite de una potencia
Límite de una función
g puede ser una raíz, un log, sen ,cos, tg, etc.
Límite de una raíz
Límite de un logaritmo
Véase más en:
3.5 LÍMITES LATERALES
Para que exista el límite de una función, deben existir los límites laterales y coincidir.
El significado de los signos en la notación para límites laterales se interpreta de la siguiente manera
- x ® a- significa que x tiende a a tomando valores menores que a, es decir valores que se encuentran a su izquierda.
- x ® a+ significa que x tiende a a tomando valores mayores que a, es decir valores que se encuentran a su derecha.
Límite lateral por izquierda
 si dado e > 0, $ d > 0 tal que
si a - d < x < a Þ
  |
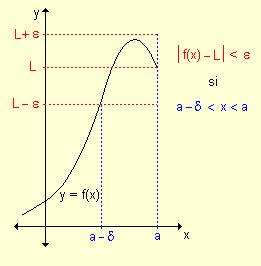Límite lateral por derecha
 si dado e > 0, $ d > 0 tal que
si a < x < a + d Þ
  |
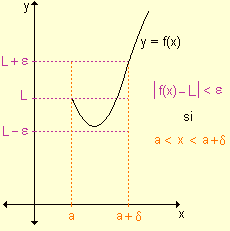Véase más en:
3.6 LÍMITES INFINITOS Y LÍMITES AL INFINITO
Límite infinito
Observemos la función f(x)=1/x2 para valores de x positivos muy grandes.
| x | f(x) |
|---|---|
| 100 | 1,0x10-4 |
| 1.000 | 1,0x10-6 |
| 10.000 | 1,0x10-8 |
| 100.000 | 1,0x10-10 |
| 1.000.000 | 1,0x10-12 |
Si tomamos x cada vez mayor, f(x) está cada vez más cerca de 0. Si x es suficientemente grande podemos conseguir que f(x) se acerque a 0 tanto como queramos. Decimos que f(x) tiende a 0 cuando x tiende a infinito.
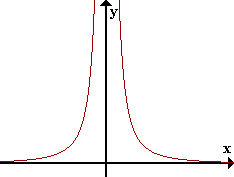
A veces podemos no usar infinito directamente, pero sí podemos usar un límite.
| Lo que pasa en ∞ es indefinido... | 1/∞ |  |
| ... pero sabemos que 1/x va hacia 0 cuando x va hacia infinito |  |  |
Límites al ir a infinito
¿Cuál es el límite de esta función?
y = 2x
Está claro que cuando "x" se hace más grande, le pasa lo mismo a "2x":
| x | y=2x |
|---|---|
| 1 | 2 |
| 2 | 4 |
| 4 | 8 |
| 10 | 20 |
| 100 | 200 |
| ... | ... |
Así que cuando "x" va a infinito, "2x" también va a infinito. Lo escribimos así:
Ver más en:
3.7 ASINTOTAS
Las asíntotas son rectas a las cuales la función se va acercando indefinidamente. Hay tres tipos de asintotas:
1. Asíntotas horizontales
Ejemplo
Calcular las asíntotas horizontales de la función:
2. Asíntotas verticales
Consideramos que el resultado del límite es ∞ si tenemos un número real partido por cero.
K son los puntos que no pertenecen al dominio de la función (en las funciones racionales).
Calcular las asíntotas verticales de la función:
Asíntotas oblicuas
Sólo hallaremos las asíntotas oblicuas cuando no haya asíntotas horizontales.
Para que haya asíntota oblicua se tiene que cumplir que el grado del numerador sea exactamente un grado mayor que el del denominador.
Ejemplo
Calcular las asíntotas de la función:
Asíntotas horizontales
Asíntotas verticales
Asíntotas oblicuas
Más información en:
3.8 FUNCIONES CONTINUAS Y DISCONTINUAS EN UN PUNTO Y EN UN INTERVALO.
Continuidades
Una función es continua en un punto si existe límite en él y coincide con el valor que toma la función en ese punto.
Una idea intuitiva de función continua se tiene al considerar que su gráfica es continua, en el sentido que se puede dibujar sin levantar el lápiz de la hoja de papel.
Continuidad de una función en un punto
Se dice que una función f(x) es continua en un punto x = a si y sólo si se cumplen las tres condiciones siguientes:
1. Que el punto x= a tenga imagen.
2. Que exista el límite de la función en el punto x = a.
3. Que la imagen del punto coincida con el límite de la función en el punto.
Si una función no es continua en un punto x=a, diremos que es discontinua en dicho punto.
Una función es continua por la derecha en un punto si existe el límite por la derecha en él y coincide con el valor que toma la función en ese punto, es decir
Una función es continua por la izquierda en un punto si existe el límite por la izquierda en él y coincide con el valor que toma la función en ese punto.
as1dda
Discontinuidades
1.- Una función es discontinua en un punto cuando no existe límite en él o, existiendo, no coincide con el valor de la función en el mismo.
2.- Una función tiene una discontinuidad evitable en un punto cuando existe límite en él y no coincide con el valor de la función en elmismo.El valor que deberíamos dar a la función en dicho punto para que fuera continua en él se llama verdadero valor de la función en el mismo.
3.- Una función tiene una discontinuidad inevitable.
Ver más en:
3.9 TIPOS DE DISCONTINUIDADES
Existen tres tipos de discontinuidad:
1. Discontinuidad evitable
Una discontinuidad es evitable en un punto x = a si existe
y éste es finito.Nos encontramos con dos tipos de discontinuidad evitable:
1. La función no está definida en x = a.
2. La imagen no coincide con el límite.
Cuando una función presenta una discontinuidad evitable en un punto se puede redefinir en dicho punto para convertirla en una función continua.
La dos funciones estudiadas anteriormente las redefinimos de modo que:
2. Discontinuidad inevitable
Una discontinuidad es inevitable o de primera especie si existen los límites laterales en x = a, pero son distintos.
Salto es la diferencia en valor absoluto de los límites laterales.
Según el tipo de salto nos encontramos con dos tipos de discontinuidad inevitable:
1. Discontinuidad inevitable de salto finito
La diferencia entre los límites laterales es un número real.
En x = 2 hay una discontinuidad inevitable de salto finito 3.
2. Discontinuidad inevitable de salto infinito
La diferencia entre los límites laterales es infinito.
En x = 2 hay una discontinuidad inevitable de salto infinito.
3. Discontinuidad esencial
Una discontinuidad es esencial o de segunda especie si no existe alguno de los límites laterales en x = a.
En x = 2 hay una discontinuidad esencial porque no tiene límite por la derecha.
En x = 2 hay una discontinuidad esencial porque no tiene límite por la izquierda.
Para más información:
http://www.ditutor.com/limites/discontinuidad.html
No hay comentarios:
Publicar un comentario