domingo, 5 de octubre de 2014

UNIDAD 1

UNIDAD 1: NÚMEROS REALES

 1.1 LA RECTA NUMÉRICA
La recta numérica es un gráfico unidimensional de una línea recta en la que los números enteros son mostrados como puntos especialmente marcados que están separados uniformemente.


Bibliografía:
http://es.wikipedia.org/wiki/Recta_num%C3%A9rica 

1.2 NÚMEROS REALES

 ¿Qué es un Número Real?

Número real  (designado por ℝ), cualquier número racional o irracional. Los números reales pueden expresarse en forma decimal mediante un número entero, un decimal exacto, un decimal periódico o un decimal con infinitas cifras no periódicas.
El conjunto de los números reales

Número Naturales (N): números con los que contamos (también se les llama enteros positivos. )

Enteros (E): conjunto de todos los números naturales con sus opuestos (negativos) y el cero. .

Racionales: conjunto formado por todos los números que se pueden escribir en la forma , donde m y n son enteros .

Número Reales (R): todos los racionales y los irracionales. Los números racionales tienen representaciones decimales repetitivas (periódicas), en tanto que los irracionales tienen representaciones no repetitivas infinitas.


Representación geométrica
Se pueden representar sobre una recta del siguiente modo: a uno de los puntos de la recta se le asocia el cero, 0. Se toma hacia la derecha otro punto al que se asocia el 1. La distancia del 0 al 1 se denomina segmento unidad y con ella se representan todos los números enteros.








 Los restantes números reales (racionales o irracionales) se sitúan sobre la recta, bien valiéndose de construcciones geométricas exactas, bien mediante aproximaciones decimales. Es importante el hecho de que a cada punto de la recta le corresponde un número real y que cada número real tiene su lugar en la recta (correspondencia biunívoca). Por eso a la recta graduada de tal manera se la denomina recta real.


Bibliografía:
http://www.eplc.umich.mx/salvadorgs/matematicas1/contenido/CapI/1_5_Numeros%20Reales.htm


 1.3 PROPIEDADES DE LOS NÚMEROS REALES 

Propiedad de la cerradura

La propiedad de la cerradura dice que puedes sumar o multiplicar dos o más números reales, y el resultado será siempre un número real.  Por ejemplo:
2,7 \in \mathbb {R}, \; \; 2+7=9, \; \; 9 \in \mathbb {R}
2,7 \in \mathbb {R}, \; \; 2 \cdot 7=14, \; \; 14 \in \mathbb {R}

Propiedad conmutativa

La propiedad conmutativa para la adición y la multiplicación dice que puedes cambiar el orden de los sumados o de los factores y el resultado será siempre el mismo. Por ejemplo:
6+7=7+6=13
6 \cdot 7=7 \cdot 6=42

Propiedad asociativa

La propiedad asociativa para la adición y la multiplicación nos permite hacer sumas o multiplicaciones parciales agrupando los sumandos o los factores para después sumar o multiplicar los resultados parciales para facilitar el cálculo de una expresión. Por ejemplo:
3+(4+5)=(3+4)+5=12
3 \cdot (4 \cdot 5)=(3 \cdot 4) \cdot 5=60

Propiedad distributiva

La propiedad distributiva tiene que ver con re ordenar o re organizar las operaciones de adición y multiplicación en una expresión, con el fin de facilitar  las operaciones aritméticas.
3 \cdot (4+5)=(3 \cdot 4) + (3 \cdot 5)=27

Propiedad de identidad (elemento neutro)

La propiedad de identidad para la adición dice que existe un número (llamado elemento neutro de la adición) que al ser usado como sumando no cambia el resultado de la suma:
25+0=25, el elemento neutro de la adición es el número CERO.
La propiedad de identidad para la multiplicación dice que existe un número (llamado elemento neutro de la multiplicación) que al ser usado como factor no cambia el resultado de la multiplicación:
25 \cdot 1=25, el elemento neutro de la multiplicación es el número UNO.

Propiedad del inverso

La propiedad del inverso aditivo, dice que existe un número que al ser usado como sumando hace que el resultado de la suma sea igual a CERO.
28+(-28)=0   el inverso aditivo para esta suma es el número -28
La propiedad del inverso multiplicativo, dice que existe un número que al ser usado como factor hace que el resultado de la multiplicación sea igual a UNO.
28 \cdot \left ( \frac{1}{28} \right )=1,   el inverso multiplicativo para esta multiplicación es \frac{1}{28}

Propiedad
Operación
Definición
Que dice
Ejemplo
Conmutativa
Suma

Multiplicación
a+b = b+a

ab = ba
El orden al sumar o multiplicar reales no afecta el resultado.
2+8 = 8+2

5(-3) = ( -3)5

 Propiedad
Operación
Definición
Que dice
Ejemplo
Asociativa
Suma

Multiplicación
a+(b+c)=(a+b)+c

 a(bc) = (ab)c
Puedes hacer diferentes asociaciones al sumar o multiplicar reales y no se afecta el resultado.
7+(6+1)=(7+6)+1

-2(4x7)= (-2x4)7


Propiedad
Operación
Definición
Que dice
Ejemplo
Identidad
Suma


 Multiplicación
a + 0 = a


 a x 1= a
Todo real sumado a 0 se queda igual; el 0 es laidentidad aditiva.

Todo real multiplicado por 1 se queda igual; el 1es la identidad multiplicativa.
-11 + 0 = -11


17 x 1 = 17


Propiedad
Operación
Definición
Que dice
Ejemplo
Inversos
Suma
a + ( -a) = 0
La suma de opuestos es cero.
.
15+ (-15) = 0


 Propiedad
Operación
Definición
Que dice
Ejemplo
Distributiva
Suma respecto a
Multiplicación
a(b+c) = ab + ac
El factor se distribuye a cada sumando.
2(x+8) =
2(x) + 2(8)


Bibliografía:
http://cenevalenlinea.com/estrategias/item/35-propiedades-de-los-numeros-reales.html https://sites.google.com/site/mago9292/unidad-1-numeros-reales/1-3---propiedades-de-los-numeros-reales

1.4 INTERVALOS Y SU REPRESENTACIÓN MEDIANTE 
DESIGUALDADES

 ¿QUÉ SON LOS INTERVALOS? 
Los Intervalos están determinados por dos números que se llaman extremos. En un intervalo se encuentran todos los números comprendidos entre ambos y también pueden estar los extremos.

 Intervalo abierto
Intervalo abierto, (a, b), es el conjunto de todos los números reales mayores que a y menores que b.

(a, b) = { x ∈ ℝ  / a < x < b}


Intervalo cerrado

Intervalo cerrado, [a, b], es el conjunto de todos los números reales mayores o iguales que a y menores o iguales que b.

[a, b] = {x ∈ ℝ  / a ≤ x ≤ b}

Intervalo semiabierto por la izquierda
Intervalo semiabierto por la izquierda,(a, b], es el conjunto de todos los números reales mayores que a y menores o iguales que b.
(a, b] = {x ∈ ℝ  / a < x ≤ b}
rceta

Intervalo semiabierto por la derecha

Intervalo semiabierto por la derecha, [a, b),es el conjunto de todos los números reales mayores o iguales que a y menores que b.
[a, b) = {x ∈ ℝ  / a ≤ x < b}
recta

 Cuando queremos nombrar un conjunto de puntos formado por dos o más de estos intervalos, se utiliza el signo ∪ (unión) entre ellos.


Representación GRÁFICA de intervalos :

[-3,6]      -3< x < 6  

(4,9)       4 < x < 9    


(1,+ ∞)   1 < x < + ∞


Bibliografía:
http://www.ditutor.com/numeros_reales/intervalos.html

1.5 RESOLUCIÓN DE DESIGUALDADES DE PRIMER GRADO 

CON UNA INCÓGNITA Y DE DESIGUALDADES 

CUADRÁTICAS CON UNA SOLA INCÓGNITA. 






 Ejemplo desigualdad lineal:



Ejemplo desigualdad cuadrática:


                   

1.6 VALOR ABSOLUTO Y SUS PROPIEDADES

Valor Absoluto:

El valor absoluto de un número real  a  coincide con él mismo si es positivo  ó  0,  y es igual a su opuesto si es negativo. Se representa por |a|.
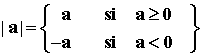
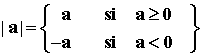
valor_absoluto

De modo que el valor absoluto de cualquier número nunca es negativo.
El valor absoluto de un número coincide siempre con el de su opuesto.


Ejemplos de valor absoluto

a) |3,5| =  3,5

b) |-1,6| = 1,6

c) |4 - 9| = |-5| = 5

d) |π - 2| = π - 2 = 1,141...

e) |-3| + |√2| = 3 + √2 = 4,414…

f) |-4,2| - |-4,2| = 4,2 - 4,2 = 0


Propiedades del valor absoluto
1. |a| = |-a|
2. |a · b| = |a| · |b|
3. |a +b | ≤ |a| + |b|           Desigualdad triangular
4. Si |a| < k                              -k < a < k

Ejemplos de las propiedades del valor absoluto

1. |-7| = |7| =7

2. |(-2) · 5| = |-10| = 10 = |-2| · |5| = 2 · 5

3. |4 + 2| = |6| = 6 = |4| + |2|

Igualmente:

|4 + (-2)| = |2| =  2  ≤ |4| + |-2| = 4 + 2 = 6

4. Si |3|<4, entonces -4 < 3 < 4



La desigualdad   |x| ≤ a   describe el intervalo cerrado    [-a , a]  , simétrico respecto al origen.

Y los números reales   |x| < a   son los del intervalo abierto    (-a, a).

La desigualdad   |x| ≥ a   describe la unión de los intervalos   (-∞ , -a] ∪ [a , ∞).

Y los números reales   |x| > a   son la unión de los intervalos abiertos     (-∞ , -a) ∪ (a , ∞).

La desigualdad   |x - c| < d   es el intervalo abierto  (c - d , c + d)  , denominado también entorno de centro   c    y   radio  d,  E(c , r).

La desigualdad   |x - c| ≤ d   es el intervalo cerrado    [c - d , c + d].

La desigualdad   |x - c| > d   es la unión de los intervalos    (-∞ , c - d) ∪ (c + d , ∞).

La desigualdad   |x - c| ≥ d   es la unión de los intervalos    (-∞ , c - d] ∪ [c + d , ∞).



Ejemplos de las propiedades del valor absoluto

A) La expresión   |x| < 5   representa el intervalo abierto  (-5, 5)

|x| < 5     ⇔     -5 < x < 5       ⇔    x ∈ (-5,5)


B) La expresión   |x| ≤ 5   representa el intervalo cerrado  [-5, 5]

|x| ≤ 5   ⇔   -5 ≤ x ≤ 5    ⇔   x ∈ [-5,5]


C) La expresión   |x-5| ≤ 7   representa el intervalo cerrado  [-2, 12]
Pues  

|x-5| ≤ 7   ⇔    -7 ≤  x - 5  ≤ 7     ⇔   - 7 + 5 ≤ x ≤ 7 + 5    ⇔     - 2 ≤ x ≤ 12   ⇔    x ∈ [-2, 12]


D) La expresión     |x| > 5     representa la unión de intervalos (-∞, -5)∪(5, ∞), 
pues

|x| > 5    ⇔   x < -5     o     x > 5    ⇔     x ∈ (-∞ , -5) ∪ (5 , ∞)


E) La expresión   |x-5| ≥ 7   representa la unión de intervalos (-∞, -2] ∪ [12 , ∞),
pues

|x-5| ≥ 7    ⇔   x-5 ≤ -7       o        x-5 ≥ 7    ⇔     x ≤ 5-7      o         x ≥ 5+7    ⇔     x ∈ (-∞ , -2] ∪ [12 , ∞)


Bibliografía:
http://calculo.cc/N%C3%BAmeros_reales/Valor_absoluto.html


1.7 RESOLUCIÓN DE DESIGUALDADES QUE INCLUYAN VALOR ABSOLUTO.





Ejemplo desigualdad con valor absoluto:






Publicado por en

No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)