UNIDAD 2

Funciones

2.1 CONCEPTO DE VARIABLE , FUNCIÓN, DOMINIO, CODOMINIO Y RECORRIDO DE UNA FUNCIÓN.


Variable:

En matemáticas y en lógica, una variable es un símbolo constituyente de un predicado, fórmula o algoritmo o de una proposición. El término «variable» se utiliza aun fuera del ámbito matemático para designar una cantidad susceptible de tomar distintos valores numéricos dentro de un conjunto de números especificado.

Tomado de: http://es.wikipedia.org/wiki/Variable_(matem%C3%A1ticas)

¿Qué es una función?

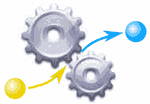Una función es como una máquina: tiene una entrada y una salida. Y lo que sale está relacionado de alguna manera con lo que entra.

Ejemplos

• "Multiplicar por 2" es una función muy simple
• La raíz cuadrada (√) es una función
• Seno, coseno y tangente son funciones que se usan en trigonometría.

Primero, es útil darle un nombre a una función. El nombre más común es "f", pero puedes ponerle otros como "g".

Y también está bien darle nombre a lo que se va adentro de la función, se pone entre paréntesis () después del nombre de la función:

Así que f(x) te dice que la función se llama "f", y "x" se pone dentro

Y normalmente verás lo que la función hace a la entrada:

f(x) = x² nos dice que la función "f" toma "x" y lo eleva al cuadrado.

Así que con la función "f(x) = x²", una entrada de 4 da una salida de 16. De hecho podemos escribir f(4) = 16.

Nota: a veces las funciones no tienen nombre, y puede que veas algo como y = x²

Tomado de: http://www.disfrutalasmatematicas.com/conjuntos/funcion.html

Dominio:

El conjunto de todos los posibles valores de ingreso que la función acepta.

Los valores de salida son llamados Rango.

Dominio -> función -> Rango

Ejemplo: si a la función f(x) = x² se le dan los valores x = {1,2,3,...} entonces {1,2,3,...} es el dominio.

Tomado de: http://www.disfrutalasmatematicas.com/definiciones/dominio-de-una-funcion.html

Codominio y Recorrido de una Función

El codominio y el rango tienen que ver con la salida, pero no son exactamente lo mismo.

El codominio es el conjunto de valores que podrían salir.

El rango es el conjunto de valores que realmente salen.Ejemplo: puedes definir una función f(x)=2x con dominio y codominio los enteros (porque tú lo eliges así).

Pero si lo piensas, verás que el rango (los valores que salen de verdad) son sólo los enteros pares.

Así que el codominio son los enteros (lo has elegido tú) pero el rango son los enteros pares.

Así que rango es un subconjunto del codominio.

Tomado de: http://www.disfrutalasmatematicas.com/conjuntos/dominio-rango-codominio.html

2.2 FUNCIÓN INYECTIVA, SUPRAYECTIVA Y BIYECTIVA


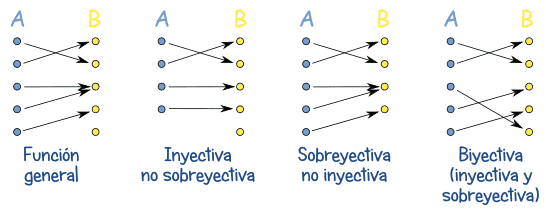
Función Inyectiva:
Una función  f: " Xà Y", es inyectiva si a cada valor del conjunto "X" (dominio) le corresponde un valor distinto en el conjunto "Y "(imagen) de "f", es decir a cada elemento del conjunto "Y" le corresponde un solo valor de "X"  tal que, en el conjunto "X" no puede haber dos o mas elementos que tengan la misma imagen.

En la figura anterior f es inyectiva y g no lo es.

O dicho de otra manera:

Una función es inyectiva si cada f(x) en el recorrido es la imagen de exactamente un único elemento del dominio. En otras palabras, de todos los pares (x,y) pertenecientes a la función, las y no se repiten.Para determinar si una función es inyectiva, graficamos la función por medio de una tabla de pares ordenados. Luego trazamos líneas horizontales para determinar si las y (las ordenadas) se repiten o no.

Tomado de: https://sites.google.com/a/itmazatlan.edu.mx/huerta/servicios-institucionales-1

Función Suprayectiva:

Suprayectiva: significa que cada elemento de "B" tiene por lo menos uno de "A" (a lo mejor más de uno). f es sobre o suprayectiva si satisface cualquiera de las siguientes condiciones:

• Para cada y en Y existe x en X tal que f(x)=y
• Y=Rf

En la figura anterior f es suprayectiva y, sin embargo g no lo es.

Función Biyectiva

Significa inyectivo y sobreyectivo a la vez. Así que hay una correspondencia perfecta "uno a uno" entre los elementos de los dos conjuntos.

Una representación de las diferentes funciones:

Tomado de: http://creandoelfuturo.net/es/funciones/funcion-inyectiva-suprayectiva-biyectiva

http://matematicasparacomputadora.weebly.com/-54-funciones-inyectiva-suprayectiva-biyectiva.html

Función Real de la Variable Real y su Representación e Irracional.

FUNCIÓN REAL DE VARIABLE REAL

Se llama función real de variable real  a toda función definida de un subconjunto D de los números reales, en el conjunto R de los números reales, tal que a cada elementox de D le corresponde uno y sólo un elemento y de R:

                                           

                                             

Para que una función quede correctamente definida es necesario determinar:

· El conjunto inicial o dominio de la función.

· El conjunto final o imagen de la función.

· La regla por la cual se asigna a cada elemento del conjunto origen un solo elemento del conjunto imagen.

Así, por ejemplo, la función definida por:

                                           

                                              

asigna a cada número real su cuadrado.

Tiene por conjunto origen o campo de existencia todos los números reales, pues dado cualquier número real x, siempre es posible calcular su cuadrado, siendo el resultado otro número real.

Tiene por conjunto imagen todos los números reales positivos, puesto que el cuadrado de un número siempre es positivo:

Más información en: http://www.sectormatematica.cl/contenidos/funreal.htm

Representación Gráfica:

Funciones Algebraicas:

Una función polinómica es aquella que está definida por un polinomio:

donde   a₀, a₁ ... a_n-1, a_n   son números reales que se llaman coeficientes del polinomioy   n   es el grado del polinomio.

Las características generales de las funciones polinómicas son las siguientes:

1) El dominio de definición es el conjunto de los números reales (R).

2) Son siempre continuas.

3) No tienen asíntotas.

4) Cortan al eje X, como máximo, un número de veces igual que el grado del polinomio.

5) Cortan el eje Y en el punto (0, a₀).

6) El número de máximos y mínimos relativos es, a lo sumo, igual al grado del polinomio menos uno.

7) El número de puntos de inflexión es, a lo sumo, igual al grado del polinomio menos dos.

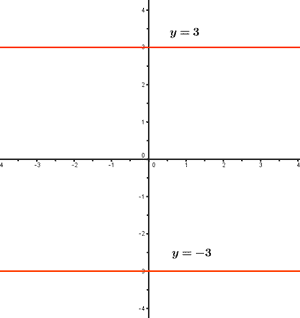
Funciones polinómicas de grado 0: rectas horizontales

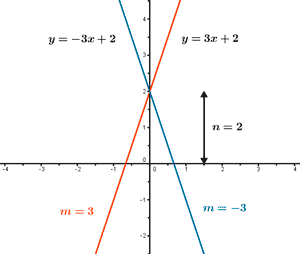
Funciones polinómicas de primer grado: rectas oblicuas

Funciones polinómicas de segundo grado:    parábolas

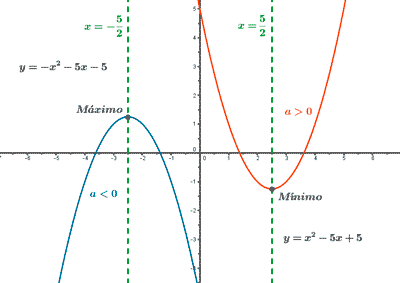
Vease más en:

 http://calculo.cc/temas/temas_bachillerato/primero_ciencias_sociales/funciones_elementales/teoria/polinomicas.html

Funciones racionales

Ir a...  Tipos funciones  Función constante -- Ejercicios interactivos  Función lineal -- Ejercicios interactivos  Función afín -- Ejercicios interactivos  Función cuadrática -- Ejercicios interactivos  Trasl. parábolas  Dilataciones  Funciones racionales  Trasl. de hipérbolas  Funciones radicales  Funciones a trozos  F. valor absoluto  Función exponencial  Fun. logarítmicas  Fun. trigonométricas  Resumen  Índice  Ejercicios I  Ejercicios II  Ejercicios III  Función lineal  Función cuadrática  Funciones  a trozos  F. valor absoluto

El criterio viene dado por un cociente entre polinomios:

El dominio lo forman todos los números reales excepto los valores de x que anulan el denominador.

Dentro de este tipo tenemos las funciones de proporcionalidad inversa de ecuación:

  .

Sus gráficas son hipérbolas. También son hipérbolas las gráficas de las función.

Más información en: http://www.vitutor.com/fun/2/c_8.html

1)   Ejemplo de función irracional:   f(x) = √x

1) Dominio:

Como   n   es par, el dominio de   f(x)   es el conjunto de valores donde   x ≥ 0 , es decir,   Dom(f) = [0, +∞)

2) Puntos de corte:

f(0) = √0 = 0  ,  es decir, el punto de corte coincide con el eje de coordenadas   (0, 0).

3) Tabla de valores:

  

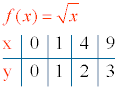
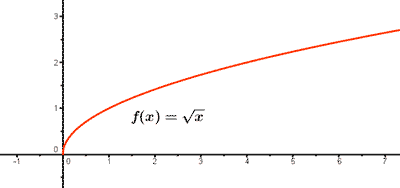
Tomado de:

 http://calculo.cc/temas/temas_bachillerato/primero_ciencias_sociales/funciones_elementales/teoria/radicales.html

2.5 FUNCIONES TRASCENDENTES: FUNCIONES TRIGONOMÉTRICAS Y FUNCIONES EXPONENCIALES.

Funcion trigonométricas

La funciones trigonométricas asocian a cada número real, x, el valor de la razón trigonométrica del ángulo cuya medida en radianes es x.

Funcion trascendentes

En las funciones trascendentes la variable independientefigura como exponente, o como índice de la raíz, o se halla afectada del signo logaritmo o de cualquiera de los signos queemplea la trigonometría.

Funciones Trigonométricas

Gráficas de las funciones trigonométricas

Seno

Coseno

Secante

Cosecante

Tangente

Cotangente

Tomado de: http://www.wikimatematica.org/index.php?title=Funciones_Trigonom%C3%A9tricas_y_sus_inversas

Funciones Exponenciales

Sea a un número real positivo. La función que a cada número real x le hace corresponder la potencia a^x se llama función exponencial de base a y exponente x.

Ejemplos

x	y = 2x
-3	1/8
-2	1/4
-1	1/2
0	1
1	2
2	4
3	8

x	y = (½)x
-3	8
-2	4
-1	2
0	1
1	1/2
2	1/4
3	1/8

Más información en: http://www.vitutor.com/fun/2/c_13.html

2.6 FUNCIÓN DEFINIDA POR MÁS DE UNA REGLA DE CORRESPONDENCIA. VALOR ABSOLUTO.

Función a trozos es un nombre más general para una función que puede ser definida con la ayuda de múltiples funciones de correspondencia.

Una función f: X → Y es llamadauna función a trozos si puede ser definida con la ayuda de varias funciones lineales.

Podemos decir que tal función está definida en una serie de intervalos múltiples.

La notación general para definir una función a trozos es la siguiente,

Como se muestra en el ejemplo, punto y coma ócomas se utilizan al final de la columna.

Sin embargo, algunos los autores prefieren usar palabras como “si” o “para” en la columna derecha, y la palabra “ de lo contrario” también se puede utilizar para indicar el caso por defecto.

La gráfica de esta función también se divide en trozos, dependiendo del número de ecuaciones que se utilicen para definir la función.

Tal función es llamada de esta forma porque la definición de esta función cambia dependiendo del valor de la variable de entrada.

Aquí el uso de la palabra “a trozos” se hace para describir la propiedad de esa función, que es válida para una ecuación / pieza de la función pero no en todo el dominio de la función.

La función a trozos tiene una serie de funciones en su cuerpo, el dominio de cada una de ellas se define por separado. El gráfico del ejemplo dado previamente luciría de esta forma,

Es claro que el gráfico anterior contiene dos piezas separadas para indicar dos ecuaciones diferentes, por lo tanto representa la función como un todo.

Un caso especial de la función a trozos es la función piso que tiene un número infinito de piezas.

El valor absoluto de cualquier número es su distancia absoluta del cero, nunca es negativo dado que la distancia nunca es negativa.

A la luz de la afirmación anterior se puede decir que el valor absoluto de cualquier número es el número mismo hecho positivo.

La función de valor absoluto es generalmente una función par, ya que cualquier número y su equivalente negativo tienen los mismos valores absolutos.

Tal función es estrictamente decreciente en el intervalo (- ∞, 0] y estrictamente creciente en el intervalo [0, ∞).

Ver más en:

http://mitecnologico.com/igestion/Main/FuncionDefinidaPorMasDeUnaReglaDeCorrespondencia

Valor Absoluto:

Valor absoluto quiere decir...

... simplemente qué distancia hay de un número a cero:

"6" está a 6 de cero, y "-6" también está a 6 de cero. Así que el valor absoluto de 6 es 6, y el valor absoluto de -6 también es 6

Más ejemplos:

• El valor absoluto de -9 es 9
• El valor absoluto de 3 es 3
• El valor absoluto de -156 es 156

¡No negativos!

Así que en la práctica el "valor absoluto" significa quitar el signo negativo de delante de un número, y pensar en todos los números como números positivos.

Símbolo de valor absoluto

Para indicar el valor absoluto de algo, pones símbolos "|" a los lados, como en estos ejemplos:

|-5| = 5

|7| = 7

Restar de las dos maneras

No importa en qué orden hagas una resta, su valor absoluto siempre será el mismo:

|8-3| = 5	|3-8| = 5
(8-3 = 5)	(3-8 = -5, y |-5| = 5)

Más información en:

http://www.disfrutalasmatematicas.com/numeros/valor-absoluto.html

2.7 OPERACIONES CON FUNCIONES: ADICIÓN, MULTIPLICACIÓN, COMPOSICIÓN. 

OPERACIONES CON FUNCIONES

Las operaciones de suma, resta, multipicacion, división entre funciones y semejantes a las correspondientes efectuadas por números.

Sean f y g dos funciones reales de variables reales  y de dominios Dom(f)  y Dom(g), respectivamente

   SUMA DE FUNCIONES

Llamamos suma de f y g, a una operación real que denominamos (f+g) tal que:

(f+g)=f(x)+g(x)

Llamos función nula o función cero a aquella función que se le asigna al dominio el valor 0 como rango.

Verifiquemos:

(f+0)(x)=f(x)+0(x)=f(x)

Por lo tanto, la función nula es el elemento neutro es decir el 0 para la suma de funciones.

      RESTA DE FUNCIONES:

Llamamos resta de f y g, a una operación real que denominamos (f-g) tal que:

(f-g)=f(x)-g(x)

      PRODUCTO DE FUNCIONES:

Llamamos producto de f por g, y se expresa (f●g) a la función:

(f●g)=f(x) ●g(x)

      COCIENTE DE FUNCIONES:

Llamamos cociente de f y g a otra función que denominamos por f/g, tal que:

f/g (x)= f(x)/g(x)

Tomado de:
https://sites.google.com/site/aprenderjojo/inicio/calculo-diferencia/unidad-2/27-operaciones-con-funciones-adicin-multiplicacin-composicin

http://www.mat.uson.mx/~jldiaz/Documents/Funcion/3-funciones-operaciones-jl.pdf


2.8 FUNCIÓN INVERSA. FUNCIÓN LOGARÍTMICA, FUNCIONES TRIGONOMÉTRICAS INVERSAS.


Función Inversa

Se llama función inversa o reciproca de f a otra función f⁻¹ que cumple que:

Si f(a) = b, entonces f⁻¹(b) = a.

Veamos un ejemplo a partir de la función f(x) = x + 4

Podemos observar que:

El dominio de f⁻¹ es el recorrido de f.

El recorrido de f⁻¹ es el dominio de f.

Si queremos hallar el recorrido de una función tenemos que hallar el dominio de su función inversa.

Si dos funciones son inversas su composición es la función identidad.

(f o f⁻¹) (x) = (f⁻¹ o f) (x) = x

Las gráficas de f y f^-1 son simétricas respecto de la bisectriz del primer y tercer cuadrante.

Hay que distinguir entre la función inversa, f⁻¹(x), y la inversa de una función, .

Véase más en: http://www.vitutor.com/fun/2/a_5.html

Función Logarítmica 

La función logarítmica en base a es la función inversa de la exponencial en base a.

Ejemplos

x
1/8	-3
1/4	-2
1/2	-1
1	0
2	1
4	2
8	3

x
1/8	3
1/4	2
1/2	1
1	0
2	−1
4	−2
8	−3

Propiedades de las funciones logarítmicas

Dominio: 

Recorrido: 

Es continua.

Los puntos (1, 0) y (a, 1) pertenecen a la gráfica.

Es inyectiva (ninguna imagen tiene más de un original).

Creciente si a>1.

Decreciente si a<1.

Las gráfica de la función logarítmica es simétrica (respecto a la bisectriz 

del 1^er y 3^er cuadrante) de la gráfica de la función exponencial, ya que son 

funciones reciprocas o inversas entre sí.

Más información en: http://www.vitutor.com/fun/2/c_14.html

Funciones Trigonométricas Inversas

Las tres funciones trigonométricas inversas usadas de manera común son:

1) Arcoseno: es la función inversa del seno del ángulo.

2) Arcocoseno: es la función inversa del coseno del ángulo.

3) Arcotangente: es la funcion inversa de la tangente del ángulo.

Seno inverso

Coseno inverso

Tangente inversa

Cotangente inversa

Tomado de:  http://www.wikimatematica.org/index.php?title=Funciones_Trigonom%C3%A9tricas_y_sus_inversas

2.9 FUNCIONES CON DOMINIO EN LOS NÚMEROS NATURALES Y RECORRIDO EN LOS NÚMEROS REALES; LAS SUCESIONES INF.

Una sucesión numérica es una función cuyo dominio es el conjunto de los números naturales y cuyo recorrido está incluido en el conjunto de los números reales.

En símbolos:

                s: lN  ®  lR  /  " n Î lN: s(n) = a_n 

Es decir que:

- a₁ es la imagen del número natural 1 por medio de la sucesión

               1  ®  s(1) = a₁ 

- a₂ es la imagen del número natural 2 por medio de la sucesión

               2  ®  s(2) = a₂

                   3  ®  s(3) = a₃

De acuerdo con esta definición, cada elemento de una sucesión puede representarse como un par ordenado (n, s(n)) o bien (n, a_n). Por consiguiente, toda sucesión puede representarse gráficamente mediante un diagrama cartesiano.

Tomado de: https://sites.google.com/site/aprenderjojo/inicio/calculo-diferencia/unidad-2/29-funciones-con-dominio-en-los-nmeros-naturales-y-recorrido-en-los-nmeros-reales-las-sucesiones-infinitas

2.10 FUNCIÓN IMPLÍCITA 

	Las funciones pueden clasificarse en funciones explícitas e implícitas. Una función en la que la variable dependiente se expresa ÚNICAMENTE en términos de la variable independiente es una función explícita. La forma de estas funciones es y = f(x), y al derivarlas, la idea es encontrar y’. Por ejemplo, la función  es una función explícita.
	En los casos en los que nuestra variable dependiente no esté expresada sólo en términos de la variable independiente, se tiene una función implícita. Una expresión equivalente a  es . Esta expresión no nos presenta a y en términos de x, por lo que en este caso tenemos a la función definida de manera implícita.
	Véase más en:  http://www.bunam.unam.mx/mat_apoyo/MaestrosAlumnos/mApoyo/02/Unidad_3/a28u3t02p01.html