Calculo Diferencial

domingo, 30 de noviembre de 2014

UNIDAD 5

5. APLICACIONES DE LA DERIVADA

5.1 RECTA TANGENTE Y RECTA NORMAL A UNA CURVA EN UN PUNTO. CURVAS ORTOGONALES

La pendiente de la recta tangente a una curva en un punto es la derivada de la función en dicho punto.

Hallar la ecuación de la recta tangente a la parábola y = x² − 5x + 6 paralela a la recta 3x + y − 2 = 0.

y = −3x + 2

La pendiente de la recta es el coefeciente de la x. m = −3

Dos rectas paralelas tienen la misma pendiente.

f'(a) = 2a − 5

2a − 5 = −3a = 1

P(1, 2)

y − 2 = −3 (x − 1)y = −3x + 5

Observamos que como la recta es paralela a la dada tiene la misma.

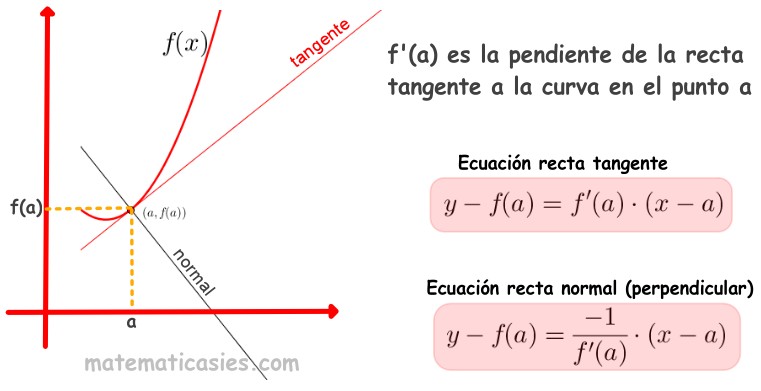
Recta tangente a una curva en un punto

La recta tangente a una curva en un punto es aquella que pasa por el punto (a, f(a)) y cuya pendiente es igual a f '(a).

Pendiente de la recta normal

La pendiente de la recta normal a una curva en un punto es la opuesta de la inversa de la pendiente de la recta tangente, por ser rectas perpendiculares entre sí.

Es decir, es la opuesta de la inversa de la derivada de la función en dicho punto.

Ecuación de la recta normal

La recta normal a a una curva en un punto a es aquella que pasa por el punto (a, f(a)) y cuya pendiente es igual a la inversa de la opuesta de f'(a).

Hallar la ecuación de la recta tangente y normal a la parábola y = x² + x + 1 paralela a la bisectriz del primer cuadrante.

La bisectriz del primer cuadrante tiene dce ecuación y = x, por tanto m = 1.

f'(a) = 2a + 1 = 1 a = 0

Punto de tangencia:(0, 1)

Recta tangente:

y − 1 = x y = x +1

Recta normal:

m= 1P(0, 1)

y − 1 = −x y = −x + 1

Curvas Ortogonales

Una tangente a una curva es una recta que toca la curva en un solo punto y tiene la misma pendiente que la curva en ese punto. Una normal a una curva es una recta que es perpendicular a la tangente de la curva. La tangente y la normal en un mismo punto en cualquier superficie siempre son perpendiculares entre sí.

Diferentes soluciones se pueden utilizar para encontrar la ecuación de la tangente de cualquier curva y = g(x) en los puntos x1, y1. La pendiente de la tangente a la curva y = g(x) en los puntos x1, y1 está dada por g‘(x1),es decir, el valor de la primera derivada de la función en x1, y1.

La ecuación requerida para esta tangente se puede encontrar en la ecuación de la recta y-y1 = m (x - x1).

Así, la ecuación de la tangente en x1, y1 se puede dar como y - y1 = g (x1) (x - x1).

Ahora bien, dado que respecto ala normalla tangente es perpendicular , su pendiente es el recíproco negativo de la pendiente de la tangente así como la pendiente de dos rectas perpendiculares son recíprocas negativas una dela otra.

Por tanto, la pendiente de la normal a la curva y = g(x) en los puntos x1, y1 es −1/g’(x1), donde g’(x1) ≠ 0.

Por lo tanto, la ecuación de la normal a la curva es dada como y – y1 = - (1/g’(x1)) (x – x1).

Si una recta tangente a la curva y = g(x) forma un ángulo Ө con el eje x en una dirección positiva, entonces la pendiente de la tangentes es igual a tan Ө.

Por tanto, la ecuación de la tangente puede ser escrita también como y – y1 = tan Ө (x – x1).

El concepto de tangente y normal contiene dos casos especiales:

1). Si la pendiente de la recta tangente es 0, entonces la recta tangente es paralela al eje x.

En tales casos, la ecuación de la tangente en el punto x1, y1 es y = y1.

2). Si la tangente es perpendicular al eje x, entonces en ese caso, la pendiente tiende al infinito y la recta tangente es paralela al eje y.

La ecuación se convierte entonces en x = x1.

Otro término importante asociado con el concepto de curva es el de las curvas ortogonales.

Cuando dos o más curvas se intersectan perpendicularmente entre sí, entonces se les conoce como curvas ortogonales.

Las tangentes de las curvas ortogonales son perpendiculares entre sí.

Además, el producto de sus pendientes es −1.

Estas propiedades pueden ser muy útiles para la determinación de curvas ortogonales.

Por ejemplo: Supongamos la recta y = (1 +

) x y la recta y = (1 -

) x

Encuentre la pendiente de y = (1 +

)x, obtenemos

dy/dx = d((1 +

)x) / dx

= 1 +

Del mismo modo, para la recta y = (1 -

)x, la pendiente resulta ser 1 -

Multiplicando la pendiente de estas dos rectas, obtenemos

m1.m2 = (1 +

). (1 -

)

 m1.m2 = - 1

Por tanto, estas dos rectas se dice que son ortogonales, es decir, se intersectan entre sí en ángulo de 90 °.

Ver más en:

http://www.vitutor.com/fun/4/k_1.html

http://www.vitutor.com/fun/4/k_2.html

http://mitecnologico.com/igestion/Main/CurvasOrtogonales

5.2 TEOREMA DE ROLLE, TEOREMA DE LAGRANGE O TEOREMA DEL VALOR MEDIO DEL CÁLCULO DIFERENCIAL.

Teorema de rolle

Si una función es:

Continua en [a, b]

Derivable en (a, b)

Y si f(a) = f(b)

Entonces, existe algún punto c pertenece

(a, b) en el que f'(c) = 0.

La interpretación gráfica del teorema de Rolle nos dice que hay un punto en el que la tangente es paralela al eje de abscisas.

Teorema del valor medio del cálculo diferencial

El teorema de valor medio, también llamado teorema de los incrementos finitos o teorema de Bonnet-Lagrange es una propiedad de las funciones derivables en un intervalo. Algunos matemáticos consideran que este teorema es el más importante de cálculo. Este teorema lo formuló Lagrange y por eso tambien el conocido como el teorema de Lagrange, es una generalización del teorema de Rolle.

Sea f(x) una función que satisface lo siguiente:

1. f(x) es una función continua en el intevalo [a,b]

2. f(x) es una funcion diferenciable en [a,b]

entonces hay un número "c" en el intervalo [a,b] tal que

${f}'_{(c)}=\frac{f_{(b)}-f_{(a)}}{b-a}$

Ver más en:

http://www.vitutor.com/fun/6/teorema_rolle.html

5.3 FUNCIÓN CRECIENTE Y DECRECIENTE. MÁXIMOS Y MÍNIMOS DE UNA FUNCIÓN. CRITERIO DE LA PRIMERA DERIVADA

Función decreciente

f es decreciente en a si sólo si existe un entorno de a, tal que para toda x que pertenezca la entorno de a se cumple:

Si f es derivable en a:

Función creciente

f es creciente en a si sólo si existe un entorno de a, tal que para toda x que pertenezca la entorno de a se cumple:

Si f es derivable en a:

Máximos y mínimos

Máximos

Si f y f' son derivables en a, a es un máximo relativo o localsi se cumple:

1. f'(a) = 0

2. f''(a) < 0

Mínimos

Si f y f' son derivables en a, a es un mínimo relativo o local si se cumple:

1. f'(a) = 0

2. f''(a) > 0

Cálculo de los máximos y mínimos relativos

f(x) = x³ − 3x + 2

1. Hallamos la derivada primera y calculamos sus raíces.

f'(x) = 3x² − 3 = 0

x = −1 x = 1.

2. Realizamos la 2ª derivada, y calculamos el signo que toman en ella los ceros de derivada primera y si:

f''(x) > 0 Tenemos un mínimo.

f''(x) < 0 Tenemos un máximo.

f''(x) = 6x

f''(−1) = −6 Máximo

f'' (1) = 6 Mínimo

3. Calculamos la imagen (en la función) de los extremos relativos.

f(−1) = (−1)³ − 3(−1) + 2 = 4

f(1) = (1)³ − 3(1) + 2 = 0

Máximo(−1, 4) Mínimo(1, 0)

Ver más en:

http://www.vitutor.net/1/funciones_1.html

http://www.dervor.com/derivadas/maximos_mimimos.html

5.4 ANÁLISIS DE LA VARIACIÓN DE FUNCIONES

Cuando la variación total de cualquier función particular es finita, en ese caso, esa función se conoce como Función de Variación Acotada, que puede ser abreviada como función BV (Bounded Variation por sus siglas en inglés). El gráfico correspondiente de la función BV se dice entonces que se comporta bien en un sentido preciso. La función BV tiene amplias aplicaciones en el campo de las matemáticas, y es utilizada en algunos de los teoremas más importantes, tal como son los Teoremas de Fourier. En el caso de la funciones continuas que contienen sólo una variable, la variación acotada implica la distancia finita cubierta por un punto a lo largo del eje y. Otra clasificación establece que las funciones de variación acotada, tienen la propiedad de intervalo cerrado, son las funciones que se pueden establecer como la diferencia entre dos monótonas acotadas.

La variación Acotada de una función determinada en el intervalo [x, y] puede ser establecida como

Donde S es el conjunto acotado

La variación resulta ser infinita si el conjunto no es acotado. El supremo de S puede ser llamado también como Variación Total o sólo la variación de f y se denota como V (f; x, y) o simplemente V (x).

Existen ciertos teoremas que pueden ser útiles para el análisis de la variación de la función:

1). Si en el conjunto [x, y], la función está incrementando, en ese caso, es la función de variación acotada en el conjunto [x, y] y consecuentemente V [g [x, y]] = g(y) – g(x).

2). Si en el conjunto [x, y] la función es constante, entonces es la función de variación acotada en el conjunto [x, y] y entonces V [g [x, y]] = 0.

Por ejemplo, la función g(r) = c es una función de variación acotada constante en el intervalo [x, y].

| g (r_i) – g (r_i - 1)| = 0 por cada partición del conjunto [a, b]. Por tanto, V (g, [x, y]) = 0.

3) En el conjunto [x, y] si, g y f son las funciones de variación acotada y c es constante, en ese caso

a). g es una función de variación acotada en el intervalo [x, y].

b). g es una función de variación acotada en cada subintervalo cerrado del intervalo [x, y].

c). cg es también una función BV en el conjunto [x, y].

d). g + f y g –f son BV en el conjunto [x, y]

e). gf es también BV en el conjunto [x, y].

Algunos datos más útiles acerca de estas funciones especiales se pueden establecer como que una función de variación acotada se puede expresar también por la divergencia de 2 funciones crecientes.

Del mismo modo, todas las funciones totalmente continuas son de naturaleza BV, sin embargo, no es necesario que todas las funciones continuas BV deban ser totalmente continuas.

La función f puede ser considerada como BV en el conjunto [x, y] si, la derivada de f se encuentra acotada en [x, y]. Además, cuando dos funciones variación acotada se multiplican entre sí, entonces la resultante es también una función de variación acotada.

Hay algunas propiedades básicas que son seguidas por las Funciones de Variación Acotada:

1) Las Funciones de Variación Acotada pueden tener discontinuidad de primer tipo, es decir, discontinuidad de salto.

Ver más en:

http://mitecnologico.com/igestion/Main/AnalisisDeLaVariacionDeFunciones

5.5 CÁLCULO DE APROXIMACIONES USANDO LA DIFERENCIAL

Se define en esta sección el concepto de la diferencial, que nos permite representar la derivada como un cociente y hallar el valor aproximado de la variación de una función alrededor de un punto.

La definición esta motivada por el siguiente razonamiento geométrico. Sea P(x0, y0) un punto fijo sobre la gráfica de y = f (x) Tomando el punto P(x0, y0) como origen, se introduce un nuevo sistema de coordenadas cuyos ejes dx y dyson paralelos a los ejes antiguos.

En este nuevo sistema de coordenadas, la recta tangente en el punto P pasa por el origen y en consecuencia, su ecuaci¨®n es bastante simple, a saber: dy = mdx, donde m es la pendiente. Ahora, como la pendiente en el nuevo sistema es la misma que la del antiguo, esto es m = f ¡¯(x), se tiene entonces: dy = f ¡¯(x) dx Lo anterior nos permite dar la definición formal de las diferencial.

Ver en:

https://sites.google.com/site/aprenderjojo/inicio/calculo-diferencia/unidad-5-aplicaciones-de-derivada/55-clculo-de-aproximaciones-usando-la-diferencial

5.6 PROBLEMAS DE OPTIMIZACIÓN Y DE TASAS RELACIONADAS

La optimización se refiere al tipo de problema que se ocupa de la determinación de la forma más apropiada para realizar cierta tarea. Con el fin de resolver estos problemas, se calculan los valores mínimos y máximos de la función. Estos incluyen encontrar la distancia mínima para llegar a un punto, el costo mínimo para hacer determinada operación, etc. La función cuyo máximo o mínimo necesita determinase por lo general está sujeta a ciertas restricciones que deben tomarse en cuenta.

Estos problemas son diferentes a los problemas utilizados para encontrar los valores mínimos o máximos locales. Los Problemas de optimización sólo se ocupan de los valores máximos o mínimos que una función puede tomar y no del mínimo o máximo en un intervalo. Es decir, la optimización busca el mínimo o máximo global (absoluto) y no el local. El mínimo o máximo absoluto es el mayor entre el mínimo o máximo local, respectivamente.

Puede haber casos, donde el mínimo o máximo global no existe para una función. En estos el dibujo de la gráfica para la función correspondiente puede ayudar en gran manera.

Hay algunos pasos que deben seguirse con el fin de desglosar un problema de optimización:

1). Lo primero y más importante es identificar las variables y constantes de la función. Esto ayuda a determinar la parte de la función que será minimizada o maximizada.

2). Escribir la fórmula adecuada para la función particular, para lo cual tenemos que calcular el mínimo o máximo.

3). Ahora, la fórmula será escrita en términos de una sola variable, es decir, f®.

4). Establezca la diferenciación de f® a 0, f ‘® = 0, y resuelva a través de observar todas las limitaciones y otros valores críticos para encontrar los valores extremos.

Por ejemplo, considere la función, g ® = -r2 + 4r – 2. Y siendo el intervalo en el cual el valor máximo será encontrado [0, 1]. Calculando g ‘® se obtiene,

g’ ® = −2r + 4 = 0

Por lo tanto, 2 viene a ser un valor crítico, luego reemplazando el 2 en la función g (2) = 2. Ahora sustituyendo uno por uno los valores del intervalo en el lugar de r, obtenemos,

g (0) = −2 g (1) = 1

Se puede observar, que el valor máximo de g® en [0, 1] es 2.

Un tipo parecido de problema es el problema de las tasas relacionadas. Se trata de un problema en el que se proporciona la tasa de variación de al menos una variable de la función y en el problema se necesita buscar la otra tasa de variación.

También hay ciertas reglas simples para resolver estos problemas:

Considere que f(a) sea una función con dos variables a y b, las cuales cambian con el tiempo y la tasa de variación de a es dada con el tiempo, es decir,

1). En primer lugar, encontrar la derivada de f(a), es decir, f ‘(a)

2). Ponga el valor de a en la ecuación

3).Entonces multiplíquelo con

para obtener

Aplicar las reglas en un ejemplo proporcionará una mejor comprensión:

Suponga que la pregunta dada dice lo siguiente: Se está bombeando aire a un globo esférico de 4 cm de radio a 5 cm3 / seg. Entonces, el ritmo de cambio del radio del globo necesita ser calculado.

Se puede observar que el radio y el volumen son las variables de las funciones correspondientes.

es dada y es igual a 5 cm3/seg y necesita encontrarse. Como

V= 4 r3 / 3. Diferenciando ambos lados, se obtiene

. Ahora sustituyendo el valor de en esta ecuación, se obtiene

  cm /seg.

Ver en:

http://www.mitecnologico.com/igestion/Main/ProblemasDeOptimizacionYProblemasDeTasasRelacionadas

UNIDAD 4

DERIVADAS

4.1 CONCEPTOS DE INCREMENTO Y DE RAZÓN DE CAMBIO. LA DERIVADA DE UNA FUNCIÓN

La derivada de una función es un vector que apunta hacia la dirección donde la función ve un mayor incremento en su valor.

A la luz de la afirmación anterior se puede concluir que la derivada de la función es generalmente cero en algunos mínimos locales o máximos locales dado que en esa posición la función no notaincrementos hacia una dirección en particular.

En algunos lugares la palabra gradiente también se usa para denotar la derivada de la función.

Sin embargo, esta palabra es más apropiada para la derivada de la función de un vector o para una función con múltiples variables.

El símbolo griego delta, representado como un triángulo es utilizado para mostrar el cambio en el valor de una variable. y significaría un cambio en el valor de y.

La pendiente de una línea recta se puede calcular como

La expresión anterior se denomina como cociente de la diferencia. Esto se debe a que representa la diferencia entre dos cocientes.

La tasa o razón de cambio puede ser constante o no. Una tasa de cambio constante es aquella que no cambia durante un período de tiempo.

Supongamos que la tasa de cambio del número de migrantes de los años 1978 a 1988 es 2.16 mientras que es de 6.9 desde el año 1988 a 2008.

Así podemos notar que en el ejemplo anterior la tasa de cambio no es constante. En tal situación se puede calcular una tasa de cambio promedio en un intervalo.

Una fórmula general para representar una tasa de cambio promedio en un intervalo sería,

Aquí y es una función en términos de t, representando la ecuación y = f (t). El intervalo es considerado entre t = a y t = b.

Si la tasa de cambio es constante durante todos los intervalos, entonces tal función es llamada función lineal.

Si la tasa de cambio de una función se calcula sobre un tipo de intervalo o en un punto específico, entonces la llamamos tasa de cambio instantánea.

La tasa de cambio de una función g en un punto x, llamada la razón o tasa instantánea de cambio en x es el límite de la tasa promedio de variación de g a lo largo de intervalos cada vez más pequeños alrededor de x.

Como sabemos la variación en la tasa es un cociente de la diferencia, la tasa instantánea de cambio será el límite de esos cocientes.

La tasa de cambio instantánea es popularmente conocida por el nombre de derivada.

No es posible calcular la derivada de una función en algún instante determinado, por tanto la derivada de una función se calcula sobre un intervalo, aunque este intervalo sea muy pequeño.

Entonces el cálculo de la derivada de una función también se puede hacer mediante el cálculo de la tasa promedio de cambio en intervalos más cortos.

Considere a el tamaño del intervalo, entonces la tasa promedio de variación en el intervalo x + a y x será,

f(x + h) – f(x)/ (x + h) – x que puede ser escrito como, f(x + h) – f(x)/ h

Ahora bien, para determinar el valor exacto de la derivada, tome el límite de la función como h. Por lo cual la derivada de la función se calcula como,

Lim f(x + h) – f(x)/ h h → 0

Para más información:
http://mitecnologico.com/igestion/Main/ConceptosDeIncrementoYDeRazonDeCambioLaDerivadaDeUnaFuncion

4.2 LA INTERPRETACIÓN GEOMÉTRICA DE LA DERIVADA

La derivada de una función en un punto es la pendiente de la recta tangente a la función en dicho punto.

Ello nos permite usar la siguiente fórmula para calcular la tangente a $f(x)$ en el punto de abcisa $x=a$ :

$y-f(a) = f'(a) \cdot (x-a)$

Análogamente podemos obtener la recta normal (perpendicular):

$y-f(a) = \frac{-1}{f'(a)} \cdot (x-a)$

Ejemplo

Halla la ecuación de la recta tangente a la curva $f(x)=x^2+2x-1$ en el punto $x=2$

La fórmula es $y-f(2) = f'(2) \cdot (x-2)$

$f(2)=2^2+2 \cdot 2 - 1 = 7$

$f'(x)=2x+2$

$f'(2)=2 \cdot 2+2 = 6$

Por tanto la ecuación es:

$\fbox{y-7 = 6 \cdot (x-2) }$

4.3 CONCEPTO DE DIFERENCIAL.INTERPRETACIÓN GEOMÉTRICA DE LOS DIFERENCIALES.

Sea f(x) una función derivable. Diferencial de una función correspondiente al incremento h de la variable independiente, es el producto f'(x) · h. Se representa por dy.

La diferencial en un punto representa el incremento de la ordenada de la tangente, correspondiente a un incremento de la variable independiente.

3. Calcular el incremento del área del cuadrado de 2 m de lado, cuando aumentamos 1 mm su lado.

S = x ²dS = 2x dx

d(S)= 2·2· 0.001 = 0.004 m²

La Interpretación Geométrica de la Derivada

Además de evaluar el valor de una función en cierto punto, también es esencial que evaluemos la variación en el valor de la función a medida que la entrada de la función varía.

Esto se conoce como la pendiente de la recta en el caso de una recta lineal. Mientras que para una recta curva, la pendiente de la recta varía en cada punto.

Esto significa que para una línea recta / función lineal se obtiene un número constante como su pendiente. Mientras que para una recta curva la pendiente es una función del valor de entrada de la función.

La noción de derivada puede explicarse de dos maneras, una como la pendiente de la curva, que es la representación geométrica, y la otra como la tasa de variación, que es la representación física. La pendiente de la tangente de la curva extrae la derivada de la función geométrica.

Supongamos que una función f(x) = x².

La gráfica de la función luciría de la siguiente forma

La curva de color azul representa el gráfico de la función.

Tome dos puntos en el eje x, supongamos x y x₀ como en el gráfico de arriba.

Determine el valor de la función en esos valores de x. Ahora trace una línea que pase por esos puntos sobre la curva de la función para obtener una línea recta.

La línea roja en el gráfico anterior representa esa línea.

A medida que muevo los puntos sobre el eje x más cerca uno del otro conseguimos una recta menos pronunciada que pasa a través de la curva de la función. En el instante que x = x₀, la gráfica se vería así,

En tal situación, la recta tocaría el grafico en un solo punto y por tanto tendría la misma pendiente que la pendiente de la gráfica en ese punto. Esta recta se conoce como la tangente de la función en ese punto.

Determinar la pendiente de la tangente en ese punto te extraerá la derivada de la función en ese punto.

La pendiente de la recta que posee los puntos(x, f(x)) y (x₀, f(x₀)) será,

Aquí el valor de x no debe ser igual a x₀.

Mientras que la pendiente de la tangente, lo que es igual, la derivada de la función, donde tenemos que x = x₀ es,

Los valores de m y m(x) son casi iguales cuando los puntos x y x₀ están muy cerca uno del otro.

Vale la pena saber que en ciertos lugares es mucho más fácil calcular el límite cuando el valor de la variable es casi igual a cero.

Podemos hacerlo mediante la traslación a lo largo del eje x.

En efecto, estableciendo el valor de h cuando x – x₀ obtenemos,

Siempre existen regiones cerca del punto de tangencia donde la curva y la recta tangente pueden simplemente compartir este punto en común.

Siempre existen regiones cerca del punto de tangencia donde la recta de tangencia deja la curva en una mitad donde se separa del plano.

Sin embargo, la pendiente de la tangente o la derivada de la función es simplemente una estimación lineal de la curva en un punto.

Ver más en:

http://www.vitutor.com/fun/4/b_12.html

http://mitecnologico.com/igestion/Main/InterpretacionGeometricaDeLasDiferenciales

4.4 PROPIEDADES DE LA DERIVADA

Las derivadas forman una parte importante del cálculo.

Hablando en términos sencillos, la derivada es una medida de la tasa de variación de la salida de una función así como varía la entrada de la función.

En base a la definición anterior está claro que la salida de la función es una función de la entrada de la función.

Las derivadas tienen algunas propiedades especiales que son importantes estudiar antes de saltar de lleno en el tema.

Puesto que estas propiedades resuelven los problemas de una manera mejor y más conveniente, con un mejor enfoque hacia el tema.

Algunas de las propiedades más importantes son las siguientes:

1. Si la función f(x): X → Y es diferenciable en un punto P, entonces se puede concluir que la función f(x) es continua en el punto p.

2. La derivada de la suma de dos funciones es igual a la suma de las derivadas de las dos funciones tomadas individualmente. La misma regla aplica también para la resta de dos derivadas. Esta regla es más conocida por el nombre de la regla de la linealidad.

3. La derivada de la multiplicación de una cantidad escalar con una función es igual a cuando la cantidad escalar se multiplica a la derivada de la misma función.

4. La derivada de un número constante es siempre igual a cero.

5. La diferenciación de una variable con respecto a si misma producirá uno.

6. La derivada de la multiplicación de dos funciones es lo mismo que sumar la multiplicación de la primera función con la derivada de la segunda función y la multiplicación de la segunda función con la derivada de la primera función. Esta regla se conoce más comúnmente con el nombre de la regla del producto.

7. La derivada de una variable elevada a una potencia es igual a las veces de la potencia de la derivada de la misma variable elevada a una potencia reducida por uno. Esta regla es mejor conocida por el nombre de la regla de la potencia. Es esencial que n sea un número real para que la propiedad anterior sea cierta.

8. La derivada de la división de una función con alguna otra función es lo mismo que la división de la resta de la multiplicación de la primera función con la derivada de la segunda función y la multiplicación de la segunda función con la derivada de la primera función con el cuadrado de la segunda función. Aquí el valor de la función no debería ser igual a cero. Esta regla se conoce por el nombre de la regla del cociente.

9. La regla de la cadena es una propiedad bastante compleja y se utiliza para funciones compuestas; es decir una función que es impuesta sobre cualquier otra función. De dos funciones diferenciables g(x) y f(x) que haya en una función compuesta h(x) se define como,

h(x) = g(f(x)) = (g 0 f)(x)

Para la función anterior h(x) la derivada puede ser calculada usando la regla de la cadena de la siguiente forma,

La Regla de la cadena sólo puede ser usada cuando existen dependencias en cadena en una función, en otras palabras, para funciones compuestas. Observe un ejemplo resuelto con la regla de la potencia,

d(5x⁴)/dx = 5[d(x⁴)/dx]

= 5(4x⁴−1)

= 5(4x³)

= 204x³

El ejemplo anterior pone de manifiesto que el uso de la propiedad hace el problema mucho más simple de resolver.

Ver más en:

http://mitecnologico.com/igestion/Main/PropiedadesDeLaDerivada

4.5 REGLA DE LA CADENA

La regla de la cadena es la fórmula resultante de la derivada de la composición de funciones.

Ejemplos

Ver más en:

http://www.dervor.com/derivadas/regla_cadena.html

4.5 FÓRMULAS DE DERIVACIÓN Y FÓRMULAS DE DIFERENCIACIÓN

Formulas de Derivación
I dc = 0
La derivada de una constante es cero
II dx = 1
La derivada de una variable con respecto a si misma es la unidad.
III d ( u + v – w ) = du + dv - dw

La derivada de la suma algebraica de un numero finito n de funciones es igual a la suma algebraica de las derivadas de las funciones
IV d ( cv ) =c. dv

La derivada del producto de una constante por una función es igual al producto de la constante por la derivada de la función
V d (uv) = u dv + v du

La derivada de un producto de dos funciones es igual al producto de la primera funcion por la derivada de la segunda, mas el producto de la segunda por la derivada de la primera.
VI d (un) = nun-1 du

La derivada de la potencia de una funcion de exponente constante es igual al producto del exponente por la funcion elevada a un exponente disminuido en una unidad y por la derivada de la funcion.
VIa d (xn ) = nxn - 1
Cuando v = x se convierte en la expresión anterior
VII d ( uv ) = v.du - u.dv.v2

La derivada de un cociente de funciones es igual al producto del denominador por la derivada del numerador, menos el producto del numerador por la derivada del denominador, todo dividido por el cuadrado del denominador VIIa d ( u/c ) = du/ c

La derivada del cociente de una función dividida por una constante es igual a la derivada de la funcion dividida por la constante

'Fórmulas de Integración y Diferenciación'

'Fórmulas de Integración y Diferenciación'

ver más en:

https://sites.google.com/site/aprenderjojo/inicio/calculo-diferencia/unidad-4/46-frmulas-de-derivacin-y-frmulas-de-diferenciacin

4.7 DERIVADAS DE ORDEN SUPERIOR Y REGLA

La derivada de cualquier función determina la tasa de variación en función de la función con respecto a la entrada de la función. Este proceso de encontrar la derivada de una función se puede aplicar en una cascada muchas veces para encontrar las derivadas de orden superior de la función. Por ejemplo, al diferenciar la derivada de primer orden de la función, uno obtendrá la derivada de segundo orden de la función y a través de la diferenciación de la derivada de segundo orden de la función obtendremos la derivada de tercer orden de la función y así sucesivamente. En términos simples diferenciar la derivada de una función dará lugar a una derivada de la función de orden superior por un grado. La derivada de primer orden de la función se representa como,

La derivada de segundo orden de una función se representa como,

La derivada de tercer orden de una función se representa como,

Y así sucesivamente. La derivada de segundo orden de la función también se conoce como “g doble prima de y”, donde g es la función en términos de y. De manera similar la derivada de tercer orden de una función también se conoce como “g triple prima de y”, etc. Las derivadas de orden superior de cualquier función pueden derivarse de esta forma hasta que la derivada obtenida es diferenciable en sí misma.

La derivada de segundo orden de una función f(x), que es todavía más diferenciable,

No es posible obtener una derivada de orden superior de la función si la derivada actual de la función no es diferenciable. Para aclarar el concepto de las derivadas de orden superior eche un vistazo al ejemplo citado a continuación. f(x) = 4×3 + 9×2 – 3x + 4 La derivada de primer orden de esta función será,

f’(x) = 12×2 +18x – 3

Por la derivada anterior ser diferenciable es posible al diferenciarla nuevamente obtener la derivada de segundo orden de la función como, f’’(x) = f’(f’(x)) = 24x + 18

Al analizar la derivada de la función anterior se puede ver que esta puede ser aún más diferenciada. Por lo tanto la derivada de tercer orden de la función será,

f’’’(x) = f‘(f’(f’(x))) = 24

Ahora la derivada de cuarto orden de la función se obtiene,

f’’’(x) = f’(f‘(f’(f’(x)))) = 0

Como se puede observar ya no es posible diferenciar la función por más tiempo, por lo tanto detenemos el proceso de diferenciación aquí.

El ejemplo anterior también arroja luz sobre un hecho muy interesante, que es, si f(x) es un polinomio con n como el más alto grado entonces la derivada de mayor orden de tal función será n +1. Una diferencia muy interesante y diminuta entre la notación convencional de la potenciación y la diferenciación se explica más adelante,

f(2)(x)= f’’(x) f2(x) = [f(x)]2

Esta es, la presencia de paréntesis en el exponente denota una operación de diferenciación, mientras que su presencia en sí denota la operación de exponenciación.

La regla de L’Hôspital, también llamada regla de Bernoulli es una parte muy importante del cálculo. Se utiliza principalmente para encontrar las salidas de los límites cuando los límites son de forma intermedia; se utiliza principalmente para las derivadas de las funciones.

Esta regla se utiliza para transformar los límites intermedios en una forma determinada y por tanto, obtener la salida más conveniente.

La definición formal de L’Hôspital es, existen dos funciones f(x) y g(x). Ahora bien, si

  , además

es real, entonces de acuerdo a la regla del L’Hôspital,

Ver más en:

http://mitecnologico.com/igestion/Main/DerivadasDeOrdenSuperiorYReglaLHopital

4.8 DERIVADA DE FUNCIONES IMPLÍCITAS

Una correspondencia o una función está definida en forma implícita cuando no aparece despejada la y sino que la relación entre x e y viene dada por una ecuación de dos incógnitas cuyo segundo miembro es cero.

Derivadas de funciones implícitas

Para hallar la derivada en forma implícita no es necesario despejar y. Basta derivar miembro a miembro, utilizando las reglas vistas hasta ahora y teniendo presente que:

x'=1.

En general y'≠1.

Por lo que omitiremos x' y dejaremos y'.

Derivar las funciones:

Cuando las funciones son más complejas vamos a utilizar una regla para facilitar el cálculo:

Ver más en:

http://www.vitutor.com/fun/4/b_11.html